Selection Sort Algorithm

In this tutorial, you will learn how selection sort works. Also, you will find working examples of selection sort in C, C++, Java and Python.

Selection sort is an algorithm that selects the smallest element from an unsorted list in each iteration and places that element at the beginning of the unsorted list.

---

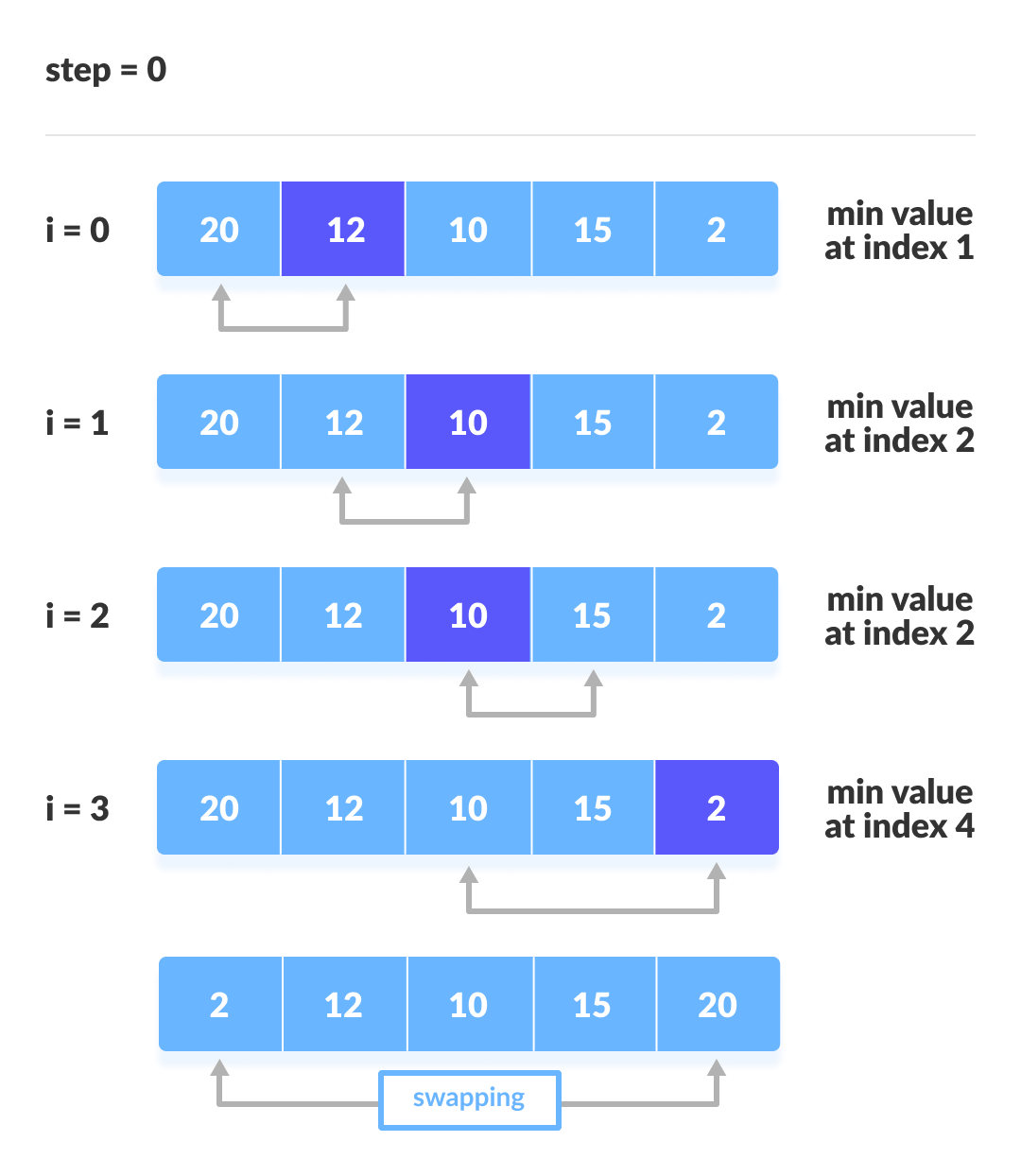
How Selection Sort Works?

1. Set the first element as minimum.
   
2. Compare minimum with the second element. If the second element is smaller than minimum, assign second element as minimum.
   
   Compare minimum with the third element. Again, if the third element is smaller, then assign minimum to the third element otherwise do nothing. The process goes on until the last element.
   
3. After each iteration, minimum is placed in the front of the unsorted list.
   
4. For each iteration, indexing starts from the first unsorted element. Step 1 to 3 are repeated until all the elements are placed at their correct positions.
     

---

Selection Sort Algorithm

selectionSort(array, size)
  repeat (size - 1) times
  set the first unsorted element as the minimum
  for each of the unsorted elements
    if element < currentMinimum
      set element as new minimum
  swap minimum with first unsorted position
end selectionSort

---

C++ Examples

// Selection sort in C++


#include <iostream>
using namespace std;


void swap(int *a, int *b)
{
  int temp = *a;
  *a = *b;
  *b = temp;
}
void printArray(int array[], int size)
{
  for (int i = 0; i < size; i++)
  {
    cout << array[i] << " ";
  }
  cout << endl;
}
void selectionSort(int array[], int size)
{
  for (int step = 0; step < size - 1; step++)
  {
    int min_idx = step;
    for (int i = step + 1; i < size; i++)
    {
      if (array[i] < array[min_idx])
        min_idx = i;
    }
    swap(&array[min_idx], &array[step]);
  }
}
int main()
{
  int data[] = {20, 12, 10, 15, 2};
  int size = sizeof(data) / sizeof(data[0]);
  selectionSort(data, size);
  cout << "Sorted array in Acsending Order:\n";
  printArray(data, size);
}

 

Complexity

Cycle	Number of Comparison
1st	(n-1)
2nd	(n-2)
3rd	(n-3)
...	...
last	1

Number of comparisons:(n-1) + (n-2) + (n-3) +.....+ 1 = n(n-1)/2 nearly equals to n2

Complexity = O(n2)
Also, we can analyze the complexity by simply observing the number of loops. There are 2 loops so the complexity is n*n = n2.
Time Complexities:

• Worst Case Complexity: O(n2)
  
  If we want to sort in ascending order and the array is in descending order then, the worst case occurs.
   
• Best Case Complexity: O(n2)
  
  It occurs when the the array is already sorted
   
• Average Case Complexity: O(n2)
  
  It occurs when the elements of the array are in jumbled order (neither ascending nor descending).

The time complexity of selection sort is the same in all cases. At every step, you have to find the minimum element and put it in the right place. The minimum element is not known until the end of the array is not reached.

Space Complexity:
Space complexity is O(1) because an extra variable temp is used.

---

Selection Sort Applications

The selection sort is used when:

• small list is to be sorted
• cost of swapping does not matter
• checking of all the elements is compulsory
• cost of writing to a memory matters like in flash memory (number of writes/swaps is O(n) as compared to O(n2) of bubble sort)